
In the second and third in this uncertainty quantification series we discussed how to estimate uncertainty by creating models able to incorporate it or by performing post-hoc calibration of traditional models. In this post we will present an alternative approach that bypasses the uncertainty quantification problem by creating an external metric with respect to the confidence in a model prediction. An example of such an approach is what was introduced as the Trust Score in this paper.
What is the Trust Score?
The idea behind the Trust Score is to have an external score to measure the confidence in a certain model prediction. In the papers the author propose a general definition of this score as —the ratio between the distance from the testing sample to the nearest class different from the predicted class and the distance to the predicted class—
The reasoning behind this proxy is quite intuitive: if there exists a point in the training set which is very close to the one we have to predict and the model agrees with the training label the trust score will tend to be higher. On the other hand, if the current prediction is very close to a point in the training set associated with a different label the score will drop.
The proposed algorithm in the paper does not define the distance metric to be used, this could be obtained for example by using an L2 distance on the raw input or, if we are in presence of a neural network, on the activation values of a certain layer. The paper does not define the number of points used to calculate the distance either.
Trust Score: a practical example
In this blog we want to apply the concept of Trust Score to the model we worked with in the previous posts, a binary classification model trained on the Lending Club dataset.
The fact that we are working with a mixed type tabular dataset introduces a first obstacle: what kind of distance measure should we use to calculate the score? The presence of few mixed ordinal and categorical columns makes it difficult to use standard similarity measures which tend to focus on either data type.
Therefore, we decided to take a different approach: we first train a Variational AutoEncoder on the dataset and then we use the latent space to calculate distances between points. We used an euclidean distance calculated w.r.t. the closest point in agreement with the classifier and the closest in disagreement.
In essence, we trained the VAE on the training set and used the Trust Score algorithm to calculate it for the test dataset. The figure below shows the distribution of the Trust Score for the test dataset.
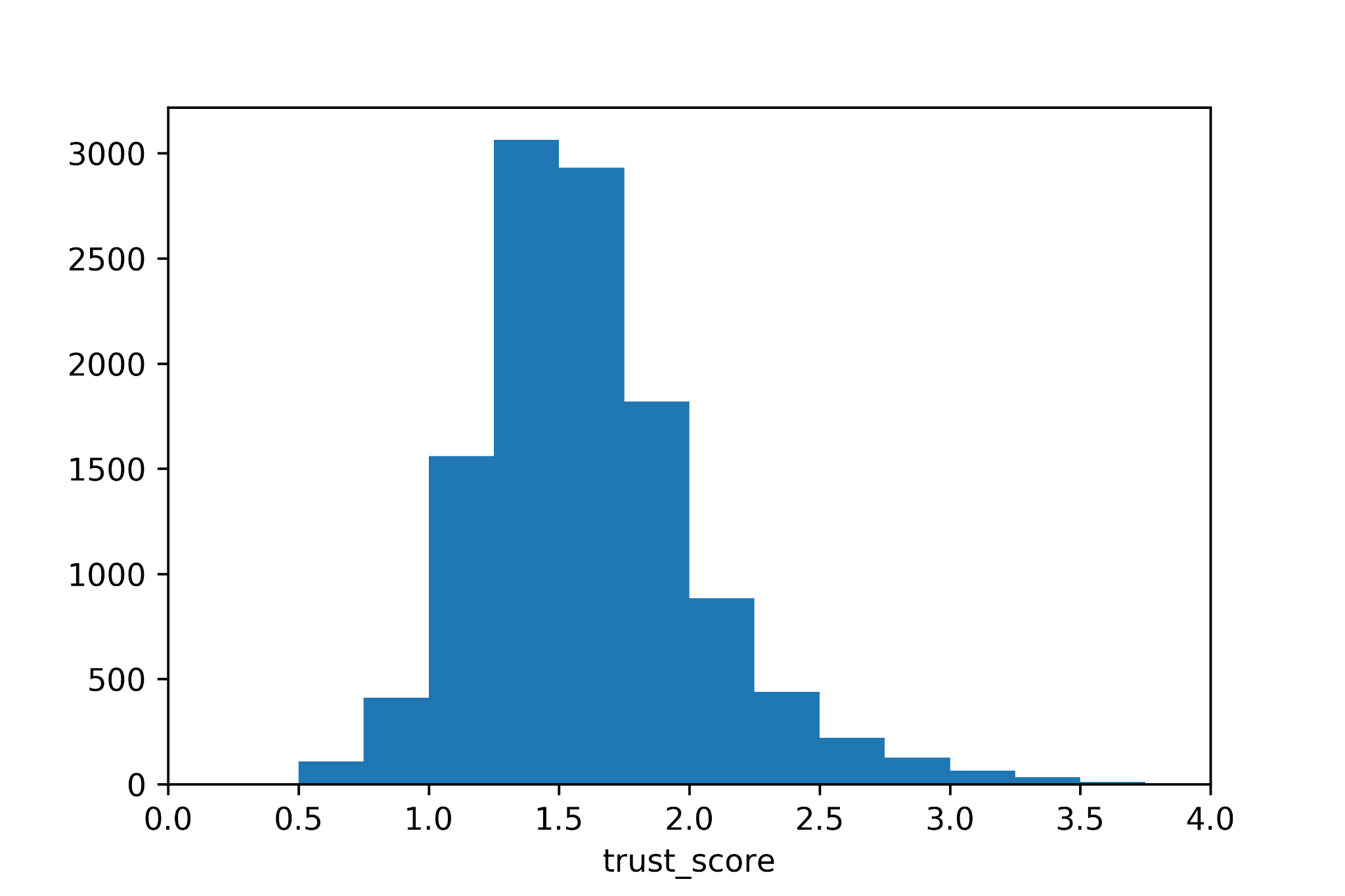
A first observation is that by definition the Trust Score is not bounded and it can take values between 0 and +infinity. This means that the definition of low or high scores is not trivial. In the original paper the authors use percentile values that can be taken for example from the distribution above.
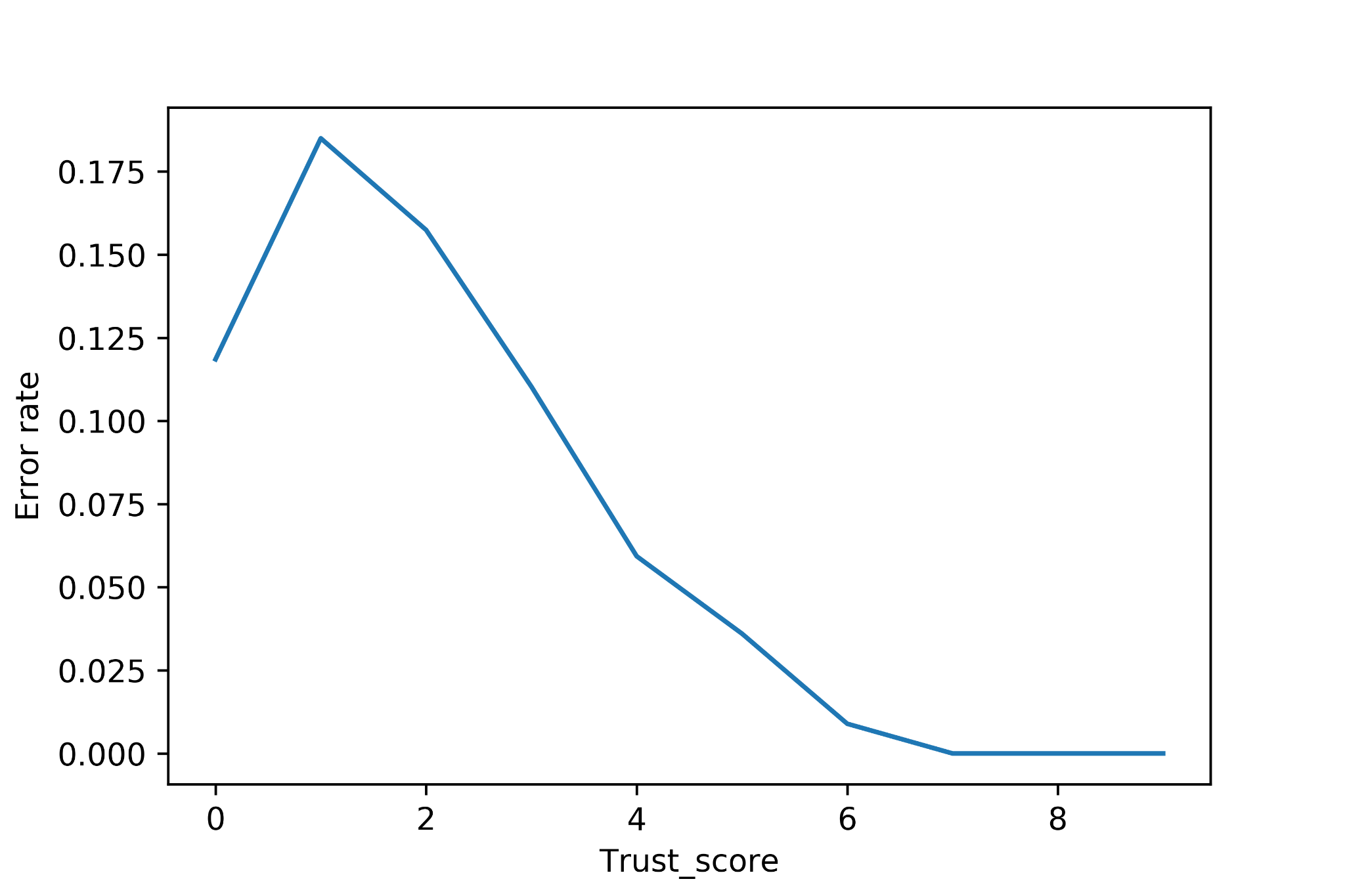
In the plot below we show how the model error rate decreases as one should expect when the Trust Score increases. As suggested in the original paper, when the Trust Score is high the classifier will agree with a Bayes-optimal classifier.
In the next figure we show the Trust Score value for the points classificated as False Positives together with the model confidence corresponding to each of these points.
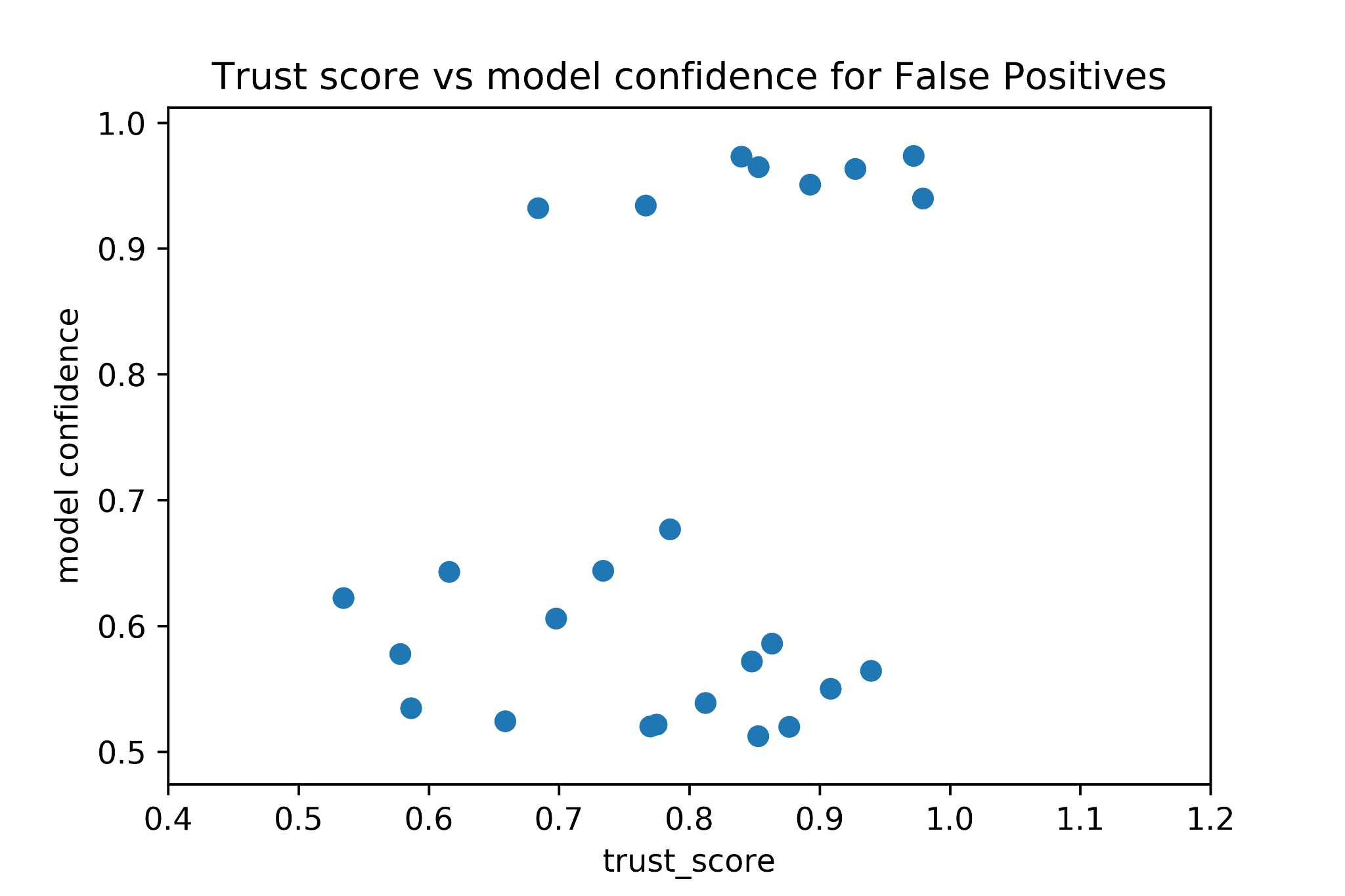
It is interesting to observe the group of points at the top part of the scatter plot. Even though the classification was wrong the model confidence for these points was considerably high while the corresponding trust score remained fairly low. This is a good example of how this kind of score could be integrated into a Decision Support System to detect when the model is too overconfident.
Trust in ML systems is a complex issue, and we need multi-faceted approaches to create and sustain it. Based on the observations we made in this post we can state that while trust score by itself might not completely replace robust uncertainty estimates given some ambiguity in its definition, it can complement it by representing a useful and distinct perspective to increase trust in model decisions.
Tags:
tutorial Luca Gilli, PhD, is CTO and co-founder of Clearbox AI, where he leads R&D and product development. Expert in generative AI, uncertainty quantification, and ML model validation, he is the inventor of Clearbox AI’s core synthetic data technology.
Luca Gilli, PhD, is CTO and co-founder of Clearbox AI, where he leads R&D and product development. Expert in generative AI, uncertainty quantification, and ML model validation, he is the inventor of Clearbox AI’s core synthetic data technology.